Matriks Dan Operasi Matriks

Matriks didefinisikan sebagai susunan persegi panjang dari bilangan– bilangan real yang diatur dalam baris dan kolom. Bilangan–bilangan tersebut dinamakan unsur dalam matriks.

Matriks ditulis sebagai berikut :

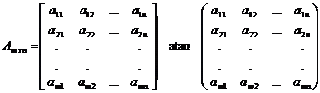
susunan diatas disebut sebuah matriks mxn karena memiliki m baris dan n kolom, dan a_ij bilangan real untuk semua i = 1, 2, . . ., m dan semua j = 1, 2, . . . , n.

Suatu matriks dikatakan sama jika keduanya mempunyai ukuran yang sama dan anggota-anggotanya yang berpadanan sama. Dalam notasi matriks, jika A = [a_ij] dan B = [b_ij] mempunyai ukuran yang sama maka A = B jika dan hanya jika (A)_ij = (B)_ij, atau setara a_ij = b_ij untuk semua i dan j.

contoh:

Definisi 1.1 : Jika A dan B adalah matriks-matriks berukuran sama,maka jumlah A + B adalah matriks yang diperoleh dengan menambahkan anggota-anggota B dengan anggota-anggota A yang berpadanan, dan selisih A - B adalah matriks yang diperoleh dengan mengurangkan anggota-anggota A dengan anggota-anggota B yang berpadanan. Matriks-matriks berukuran berbeda tidak bisa ditambahkan atau dikurangkan.

Definisi 1.2 : jika A adalah sembarang matriks dan c adalah sembarang skalar,maka hasil kali cA adalah matriks yang diperoleh dengan mengalikan setiap anggota A dengan c.

Sifat – sifat operasi matriks :

1. A + B = B + A (hukum komutatif)

2. A + (B + C) = (A + B) + C (hukum asosiatif penjumlahan)

3. a (B + C) = aB + aC dimana a suatu skalar

4. (a + b) C = aC + bC dimana a dan b suatu skalar

5. (ab) C = a(bC) dimana a dan b suatu skalar

6. a(AB) = (aA)B = A(aB) dimana a suatu skalar

7. A(BC) = (AB)C (hukum asosiatif pada perkalian)

8. A(B+C) = AB + AC (hukum distributif)

9. (A + B)C = AC + BC (hukum distributif)

Matriks Transpose

Definisi 1.3 : Jika A adalah sembarang matriks m x n, maka transpos A, dinyatakan dengan A^T, didefinisikan sebagai matriks n x m yang didapatkan dengan mempertukarkan baris dan kolom dari A.

Sebagai contoh:

Sifat – sifat matriks transpose :

a. ((A)^T)^T = A

b. (A + B)^T = A^T + B^T dan (A – B)^T = A^T - B^T

c. (kA)^T = kA^T dengan k adalah sembarang scalar

(AB)^T = B^TA^T

Sumber : Selvia Lorena Br. Ginting, S.Si., MT, Unikom