Misalkan A adalah matriks kuadrat maka determinan matriks tersebut dinyatakan dengan det(A) atau | A |. Determinan A dikatakan berordo n, jika A merupakan matriks kuadrat berordo nxn.
Cara menghitung nilai determinan suatu matriks :
1. Determinan Matriks berordo Satu
Misalkan A adalah matriks bujursangkar berordo 1
A = [a11], maka det A = | A | = a11
2. Determinan Matriks berordo dua dan tiga (2x2, 3x3)
Determinan matriks yang berordo 2x2 didefinisikan sebagai :
Sebagai contoh :
Determinan dari matriks  adalah:
adalah:
Determinan matriks yang berordo 3x3
contoh :

Sebagai contoh :


Catatan : Cara Sarrus hanya boleh digunakan pada matriks 3 x 3
2. Nilai Determinan dengan Kofaktor
Untuk mencari nilai matriks berordo nxn dapat diselesaikan dengan cara menggunakan kofaktor, tetapi haruslah dikenal dulu minor dari elemen matriks. Minor dari elemen aij, dimana aij merupakan satu elemen dari matriks kuadrat A, dinyatakan oleh Mij dan didefinisikan sebagai determinan dari bagian matriks A diluar baris ke-i dan kolom ke-j. Bilangan (-1)i+j . Mij dinyatakan dengan cij dan disebut kofaktor dari elemen aij :
cij = (-1)i+j . Mij
Determinan dari matriks kuadrat A dengan ordo nxn dapat dihitung dengan mengalikan elemen-elemen dalam suatu baris (atau kolom) dengan kofaktor-kofaktornya dan menambahkan hasil-hasil kali yang dihasilkan, yakni untuk setiap 1<= i <= n dan 1<= j <= n , maka :

(ekspansi kofaktor sepanjang kolom ke j), dan

ekspansi kofaktor sepanjang baris ke i)
Sebagai contoh :

a) Dengan mempergunakan baris ke-1 (i=1)

cij = (-1)i+j . Mij
c11 = (-1)1+1 . (-8) = -8
c12 = (-1)1+2 . (0) = 0
c13 = (-1)1+3 . (4) = 4

b) Dengan mempergunakan kolom ke-1 (j=1)

cij = (-1)i+j . Mij
c11 = (-1)1+1 . (-8) = -8
c21 = (-1)2+1 . (-6) = 6
c31 = (-1)3+1 . (-3) = -3

Contoh Lain` :

Jawab :
Dengan menggunakan bari ke-1 (i=1)





Jadi det(A) = -2
Sumber : Selvia Lorena Br. Ginting, S.Si., MT, Unikom


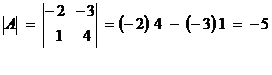

Posting Komentar